Some notes about L-systems in Houdini.

I’ve been spending a good amount of time recently on trying to figure out L-systems in Houdini. I’ve always wanted to be able to grow plants in 3D, and I was always frustrated by the lack of flexibility in Maya’s Paint Effects and the Onyx plant generator, so I figured it was time to learn this once and for all. Let’s just say there is a bit of a learning curve, like anything else in Houdini.

I’m not going to go into the basics of L-systems here, there is way too much for me to even consider posting. The best resources I’m aware of for learning how to use them in Houdini are this tutorial on Digital Tutors, and this tutorial on CmiVFX. The Digital Tutors tutorial is probably a little bit easier to start off with as it tries to take a more flexible approach to making the plants grow (as opposed to CmiVFX’s more “pure” L-systems approach) but they both require basic Houdini ability before you start.

Anyways. The plant I was trying to create was a little seedling, with leaves that unfurl as they grow out from the main stem. Here’s what I came up with:

Hit the jump to see the breakdown…

Just a little guy like this is pretty complicated. The stem needs to stop growing after a time, but the leaves need to continue growing even after the stem stops. Additionally, the leaves need to play their unfurling animation according to where they are in their growth stage. The leaves need to be arranged in pairs that are generally (but not always) opposite each other, and they need to grow out of somewhat random (but not too random) positions from the stem. The randomness is very important to making believable plants, but if you go too far then most of the plants you generate from the ruleset will look ridiculous.

On to the rules. There’s a lot of them, and it’s probably not the most efficient way to write the rules, but L-systems tend to be programmed one step at a time. You start small and then before you know it you have a huge, unreadable mess of code. It’s one of the reasons this stuff is so hard to learn; it’s very difficult to take apart someone else’s system. I’ll try to explain them as best I can.

X(h): (h>0) = /(137.5+n) ~(20) ^(rand(t)*50) T F X(h-1) : 0.7
X(h): (h>0) = /(137.5+n) ~(10) T F [~(12) &B] [/((90*rand(t))+90) ~(12) &B] X(h-1) : 0.3
B = J(0.1,0,1,rand(t))
J(m,0,r,b): (m<0.7) = J(m+0.03,0,r+2,b)
J(m,0,r,b): (m>0.7) = J(m,0,r+2,b)
X(h): (h<1) & (h>-10) = "/(137.5+n) ~(50) T F X(h-1) : 0.7
X(h): (h<1) & (h>-10) = "/(137.5+n) ~(80) T F [~(12) &B] [/(180) ~(12) &B] X(h-1) : 0.3

The variable in the premise, e, is just the number of generations that the stem will be growing for. This will make more sense in a second.

Rule 1 is telling the plant that as long as the value of h (which starts as the same value as e in the premise) is greater than zero, then we twist the stem a certain amount (137.5 degrees plus a variable n, which is animated in order to make the plant slowly twist over its whole length as it grows for a nice effect), randomly bend by up to 20 degrees, then pitch down by a certain amount (50 times a random value, seeded by the current generation t). Then the tropism value T applies a gravity force to the plant, which is actually a strong negative value (about -20) to force the plant to grow straight upwards. I did this so that the plant would randomly twist and kink a whole bunch, but still tend to grow upwards from the ground instead of twisting into itself. Finally, the stem grows forward by a straight segment, F, and another generation is appended with the value of h-1. This means each generation has a value of h one smaller than the last, so h is just a simple counter.

Rule 2 is very similar to rule 1, except that there are some branches being drawn (eventually they will be leaves). One of them is twisted randomly by up to 12 degrees, then pitched up by our default angle of about 30 degrees (defined in the “Values” tab of the L-system). The other opposing branch is rotated by a random amount, at least 90 degrees plus another 90 degrees times a random value seeded by the current generation number. Then we continue growing upwards. The 0.7 and 0.3 at the end of rules 1 and 2 just mean that 70% of the time we’re just growing upwards, but 30% of the time we draw leaves.

Rule 3 defines the basics of the leaf. It starts at a scale of 0.1. The second number is 0 because Houdini simply doesn’t use that parameter, I don’t know why it’s there. The third and fourth numbers are for stamping values to each leaf copy later on; this allows us to customize each leaf quite a bit. If you look at the “Funcs” tab of the L-system, you have Leaf Params A B and C. The third number in Rule 3 corresponds to Leaf Param A, and the fourth number is Leaf Param B. That means we can call a stamping function later on and refer to the channel “/lsystem1/paramName” to get this value. This will make a little more sense later on…  the third number will control the frame of the leaf animation, and the fourth will randomly scale the leaves slightly.

Rules 4 and 5 evolve the leaves. If the scale of the leaf is smaller than 0.7, then we increase the scale by 0.03 for each generation, add 2 to the frame of the leaf animation (again, this is for stamping, so as far as the L-system is concerned the variable does nothing. We’ll have to work some magic in SOPs to do this), and b (the random scale constant) remains the same. If the scale is greater than 0.7, we continue playing the animation forward, but we stop scaling the leaf. This way, once the leaf has reached its maximum scale, it will continue unfurling without growing any larger.

Rules 6 and 7 are a little weird… The counter h keeps decreasing for each generation even after it falls below zero. Rules 1 and 2 are no longer applying. These rules are very similar to rules 1 and 2, but they are using the “ operator to cause the stem to grow slightly less for each generation, up to 10. This just makes the stem slow down as it grows, which looks nicer than abruptly cutting off. After the counter falls below -10, these rules no longer apply and the stem stops growing.

On to the leaves. There is a single leaf geometry, which is pre-animated with a rolling animation. I used a big joint chain (about 50 of them) with an expression to cause them to roll up by one degree each, based on the joint number. Joint 1 (the root) rotated 1 degree, joint 2 rotated 2 degrees, etc. Here’s what the expression looked like for the rotateX of each joint:

opdigits(".")*chf("/obj/leaf_skeleton/null1/butt", $F-opdigits("."))

Looks hideous but it’s not so bad. The opdigits HScript command just returns any numbers that are in an object’s name, so an object named “Joint42” will return “42” (as a number, not a string). The channel named “null1/butt” (sorry I am a five-year-old) is just an arbitrary animated channel that multiplies against the number returned by opdigits. I animated this channel to start the joints all rolled up, and then unroll smoothly. chf grabs the value of this channel at a frame, specified by the current frame minus the number of the joint (again, opdigits). This causes the joints to unroll in sequence, like a carpet, instead of all unrolling at once. The last thing I did was apply a timeblend and timeshift SOP to the deforming leaf, so I could ease out the unfurling and make it all nice and smooth.

Once the leaf is connected to the J input of the L-system, I can start using all these nice stamp parameters. I apply a transform SOP to the leaf before it’s connected to the L-system, and on the uniform scale I can use this stamp expression:

fit01(stamp("../lsystem3", "leafJ_scale", 0), 0.1, 0.2)

fit01 accepts an input that is expected to range from 0 to 1, and fits it to a new range. In this case, it’s 0.1 to 0.2. It’s grabbing the parameter “leafJ_scale” from the L-system, which is the name of Leaf Parameter B, which is referred to as b in rules 4 and 5. The value is initialized in rule 3 as rand(t), which is just a random number between 0 and 1, seeded by the generation number. So, each leaf is randomly scaled slightly. Easy!

A quick aside: notice how anytime I’m defining random values in the L-system rules, I’m using the generation number t as the seed? This is actually really important. If I used something else for the seed, like a constant (2326), the random value would evaluate the same for every generation, which would form a very obvious pattern (the scale would be the same every time). If, on the other hand, I used some other changing value like $F, the leaves would constantly be rescaling themselves on every evaluation. Using t will make the random value consistent for each generation, but different between generations. There is one small problem with this, though: if the current generation isn’t a whole number, the random value will evaluate differently every frame until it is a whole number. I sidestepped this by growing the plant only with whole generation numbers (generations = $F) and using a very small step size.

To unfurl the plant, I used a timeshift SOP before the leaf plugs into the L-system. The stamp expression on the frame number here is simple:

stamp("../lsystem3", "leafJ_unroll", 0)

The parameter “leafJ_unroll” is the name of the L-system’s Leaf Param A, which corresponds to r in rules 4 and 5. The frame number of the timeshift SOP, then, starts at zero, and increases by 2 for every generation. Now the leaves unfurl as they scale up! You can create some really complex animations this way, by blending pre-animated SOPs with L-systems.

A few other quick notes. I like having visual control over the thickness of the stem, like a ramp parameter. This actually isn’t too hard to do. First, I enabled “Point Attributes” on the L-system’s Geometry tab. This creates an attribute called “width” and “arc”, among other things. The “arc” parameter can be used to figure out the total distance the “turtle” has traveled from the base of the plant to the current point. We can use the ratio between the arc length of any given point and the maximum arc to drive a ramp parameter which outputs a “width” value for each point on the curve. It sounds harder than it is. Use an Attribute Promote SOP to promote the “arc” attribute to a detail attribute with promotion method “maximum,” name it something like “maxarc,” and don’t delete the original. We can then use a VOP SOP to create the new ramp parameter. The VOP network looks something like this:

 

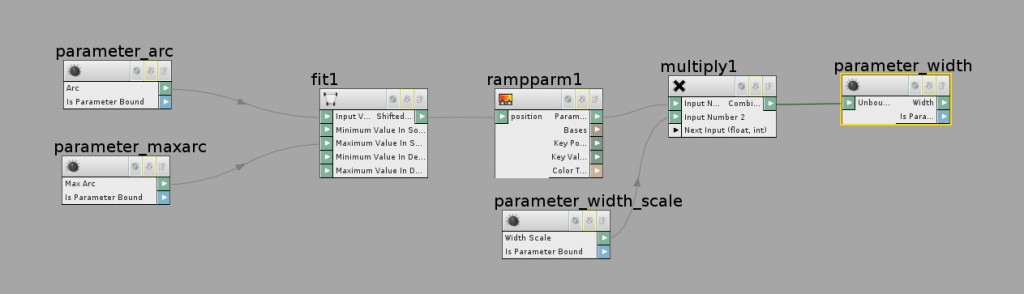
The “arc” value is brought in as a parameter, and plugs into the input value of a Fit Range VOP. The “maxarc” value is applied as the “maximum” of the Fit Range. The Fit Range VOP takes the ratio of these two values and fits them to a 0-1 range, which is perfect for driving a Ramp Parameter. The ramp is just a simple scalar ramp. This value is multiplied by another parameter, “width_scale”, so we can control our output range a little better. Then we output the “width” parameter, which can easily be read by a polyWire SOP. You can use the ramp parameter along with the width_scale control to taper the width of the stem towards the top, and animate one or both controls to have the stem thicken over time.

One last thing… let’s say you wanted to have a bunch of these plants growing at once. With some creative copy stamping, this is no problem at all. Scatter a bunch of points on a surface, and use them as the source points for a Copy SOP. Plug the plant into the geometry to copy. On the Copy SOP, we can create a few stamp variables to influence each individual plant… I created randomSeed, randomTimeOffset, and randomHeight. Each of these values are based on rand($PT), multiplied by whatever potential range you want the value to have. For example:

 randomSeed = rand($PT)*34535677

randomOffset = rand($PT)*40

randomHeight = fit01(rand($PT+1)*23092, 15, 23)

The randomHeight can control the e variable of the L-system using a stamp expression. Remember that e is what the rules use to determine when the stem is to stop growing. The randomSeed parameter controls the Random Seed of the L-system, so each instance of the plant is different. The randomOffset is to make each plant start growing at a slightly different time… instead of a random value, you could also use some other animated parameter (like an animated ramp texture connected to the color of the growth surface) to control which plants grow when. Between the L-system and the Copy SOP, insert a Time Shift SOP and use this expression for the frame:

$F-stamp("../copy1", "randomOffset", 0)

Now the plants will be delayed by a value equal to the randomOffset attribute applied to each point of the Copy SOP.

The end result looks a little like this:

Hope this was somewhat useful. L-systems are really confusing, and take a lot of practice to get comfortable with. I strongly recommend getting a hold of one or both of those tutorial videos if you want to get started with these. And, of course, here are my files to play with. Good luck…